| | | |
 Home /
Home /
Curbă închisă 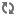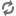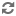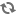 Uploading .... Uploading ....O curbă este închisă dacă există cel puţin două valori distincte ale parametrului independent pentru care curba are aceeaşi valoare. Aşadar, dacă o curbă este definită prin 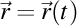 , atunci curba este închisă dacă avem , atunci curba este închisă dacă avem 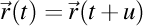 . .
Fără a pierde din generalitate, putem considera că 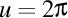 . Atunci deducem că toate funcţiile ce definesc componentele curbei închise sunt periodice de perioadă . Atunci deducem că toate funcţiile ce definesc componentele curbei închise sunt periodice de perioadă 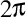 . Dar ştim că orice funcţie periodică poate fi descompusă în serie Fourier. Deci fiecare componentă a curbei este o sumă de sinusuri. . Dar ştim că orice funcţie periodică poate fi descompusă în serie Fourier. Deci fiecare componentă a curbei este o sumă de sinusuri.
Cercul este o curbă închisă, dar este o curbă plană. Orice altă curbă închisă se poate obţine din cerc prin deformarea lui, deci prin modificarea curburii şi torsiunii lui. Pentru a modifica torsiunea trebuie să „rupem” planul cercului.
Pentru orice curbă închisă există o sferă de rază minimă ce conţine acea curbă.
O elice închisă are lancretianul constant şi darbuzianul periodic. La o elice închisă vectorul lui Darboux este constant în direcţie dar variabil în modul. Mai mult, vectorul lui Darboux trebuie să-şi schimbe sensul cel puţin de două ori, altfel elicea închisă nu poate ajunge de unde a plecat. Ca să-şi schimbe sensul este necesar să se anuleze. Aşadar, vectorul lui Darboux al unei elice închise se anulează cel puţin de două ori. Când se anulează vectorul lui Darboux, se anulează şi darbuzianul. Prin urmare, într-o perioadă, darbuzianul trece prin două maxime şi prin două zerouri.
-Dacă darbuzianul este o funcţie periodică, înseamnă că el poate fi descompus în armonicele sale. Înseamnă că cea mai simplă elice închisă este elicea sinusoidală, adică elicea la care darbuzianul este sinusul parametrului canonic.
[Ipoteze]
-Se pare că atomul de hidrogen este format din doi (sau patru?) luxoni care se deplasează pe aceeaşi elice sinusoidală în aşa fel încât impulsul total şi momentul cinetic total se conservă.
-Elicea închisă ne oferă posibilitatea de a înţelege de ce electronul are simetrie de 720o, prin aceea că după o rotaţie de 360o electronul ajunge „sus” şi abia după încă o rotaţie de 360o ajunge înapoi de unde a plecat.
[/Ipoteze]
[De studiat]
-vrem să calculăm curbura şi torsiunea unei curbe închise, ale cărei coordonate sunt serii Fourier.
[/De studiat]
|
|
|
| | | |
|

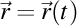 , atunci curba este închisă dacă avem
, atunci curba este închisă dacă avem 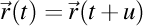 .
.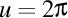 . Atunci deducem că toate funcţiile ce definesc componentele curbei închise sunt periodice de perioadă
. Atunci deducem că toate funcţiile ce definesc componentele curbei închise sunt periodice de perioadă 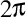 . Dar ştim că orice funcţie periodică poate fi descompusă în
. Dar ştim că orice funcţie periodică poate fi descompusă în 