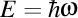Ştim că orice corp în mişcare este însoţit de un triedru Frenet, adică de un triplet de trei versori reciproc perpendiculari numiţi tangentă, normală şi binormală. Tangenta ne arată în ce direcţie se mişcă corpul dat, normala, împreună cu tangenta, ne arată planul în care se mişcă corpul, iar binormala este versorul dat de produsul vectorial al tangentei şi normalei. Evident, în timpul mişcării poziţia acestor trei versori se modifică în raport cu un reper cartezian considerat fix. Totuşi, triedrul lui Frenet în ansamblul său se comportă ca un solid rigid, pentru că poziţia relativă a versorilor, nu se poate modifica niciodată şi nu se poate modifica nici lungimea versorilor. Dar ştim că un solid rigid are, pe lângă mişcarea de translaţie şi o mişcare de rotaţie. La fel, nici triedrul lui Frenet asociat corpului în mişcare nu va fi lipsit de mişcare de rotaţie, ci dimpotrivă, el se va roti în jurul unei direcţii care este dată tocmai de vectorul lui Darboux asociat acelui triedrul Frenet.
O situaţie interesantă se naşte atunci când corpul se mişcă exact în linie dreaptă. Când corpul se mişcă în linie dreaptă, tangenta triedrului lui Frenet nu se poate modifica în timp şi ştim precis că ea indică mereu în aceeaşi direcţie. Problema este cu normala. Ce facem cu normala în cazul acesta? Normala şi binormala nu pot dispărea în neant. Ele există undeva acolo. Doar că încă nu avem mijloace clare să le putem determina. Cum facem să le putem determina în acest caz al mişcării corpului în linie dreaptă?
Primul lucru care îmi vine în minte este ciudata relaţie de proporţionalitate din mecanica cuantică în care se face legătura dintre energie şi o viteză unghiulară, adică relaţia 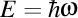
. Eu n-am înţeles ce este această viteză unghiulară aici, pentru că n-am înţeles ce este „unda asociată unei particule” dar am impresia că pot face o legătură cu consideraţiile anterioare şi, poate, prin această legătură să clarificăm ce este cu această undă asociată unei particule. Mai precis, vom lua de bună această relaţie, vom recunoaşte că mecanica cuantică ştie ea ceva despre profunzimile lumii şi vom admite împreună cu ea că energia unui corp este proporţională cu viteza unghiulară. Doar că viteza unghiulară de care vom vorbi noi va fi tocmai viteza unghiulară a triedrului Frenet asociat mişcării corpului. Aşadar, vom prelua relaţia din mecanica cuantică şi vom preciza că viteza unghiulară din această relaţie este de fapt viteza unghiulară a triedrului lui Frenet.
O situaţie interesantă se naşte atunci când corpul se mişcă exact în linie dreaptă. Când corpul se mişcă în linie dreaptă, tangenta triedrului lui Frenet nu se poate modifica în timp şi ştim precis că ea indică mereu în aceeaşi direcţie. Problema este cu normala. Ce facem cu normala în cazul acesta? Normala şi binormala nu pot dispărea în neant. Ele există undeva acolo. Doar că încă nu avem mijloace clare să le putem determina. Cum facem să le putem determina în acest caz al mişcării corpului în linie dreaptă?
Primul lucru care îmi vine în minte este ciudata relaţie de proporţionalitate din mecanica cuantică în care se face legătura dintre energie şi o viteză unghiulară, adică relaţia
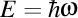
.
Eu n-am înţeles ce este această viteză unghiulară aici, pentru că n-am înţeles ce este „unda asociată unei particule” dar am impresia că pot face o legătură cu consideraţiile anterioare şi, poate, prin această legătură să clarificăm ce este cu această undă asociată unei particule. Mai precis, vom lua de bună această relaţie, vom recunoaşte că mecanica cuantică ştie ea ceva despre profunzimile lumii şi vom admite împreună cu ea că energia unui corp este proporţională cu viteza unghiulară. Doar că viteza unghiulară de care vom vorbi noi va fi tocmai viteza unghiulară a triedrului Frenet asociat mişcării corpului. Aşadar, vom prelua relaţia din mecanica cuantică şi vom preciza că viteza unghiulară din această relaţie este de fapt viteza unghiulară a triedrului lui Frenet.
. Eu n-am înţeles ce este această viteză unghiulară aici, pentru că n-am înţeles ce este
„unda asociată unei particule” dar am impresia că pot face o legătură cu consideraţiile anterioare
şi, poate, prin această legătură să clarificăm ce este cu această undă asociată unei particule.
Mai precis, vom lua de bună această relaţie, vom recunoaşte că mecanica cuantică ştie ea ceva despre profunzimile lumii
şi vom admite împreună cu ea că energia unui corp este proporţională cu viteza unghiulară.
Doar că viteza unghiulară de care vom vorbi noi va fi tocmai viteza unghiulară a triedrului Frenet asociat mişcării corpului.
Aşadar, vom prelua relaţia din mecanica cuantică şi vom preciza că viteza unghiulară din această relaţie este de fapt viteza unghiulară a triedrului lui Frenet.