| | | |
 Home /
Home /
Torsiune complexă  Uploading .... Uploading ....
Numesc torsiune complexă a unei curbe numărul complex q dat de expresia 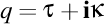 , unde , unde 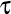 este torsiunea curbei în punctul dat, iar este torsiunea curbei în punctul dat, iar 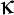 este curbura curbei în acelaşi punct. este curbura curbei în acelaşi punct.
Să observăm că argumentul torsiunii complexe este legat direct de lancretianul curbei, mai precis, avem 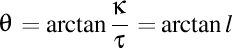 , iar modulul torsiunii complexe , iar modulul torsiunii complexe 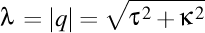 are şi el importanţa sa în Fizica elicoidală. are şi el importanţa sa în Fizica elicoidală.
Evident, în baza teoremei lui Lancret, dacă argumentul torsiunii complexe a unei curbe este constant peste tot, atunci curba respectivă este tocmai o elice, şi reciproc. Aşadar, elicelor le corespund (în planul complex al torsiunilor complexe) drepte cu centrul în origine.
Dacă torsiunea complexă a unei curbe nu are parte reală, atunci curba dată este o curbă plană, şi reciproc. De asemenea, dacă torsiunea complexă a unei curbe este un număr real, atunci curba respectivă este o dreaptă, şi reciproc.
În baza teoremei fundamentale a teoriei curbelor, oricărei curbe din spaţiul tridimensional îi corespunde o curbă din planul complex al torsiunilor complexe. De exemplu, am văzut mai sus o asemenea asociere între elicele din spaţiul tridimensional şi dreptele din planul complex al torsiunilor complexe.
|
|
|
| | | |
|

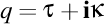 , unde
, unde 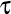 este torsiunea curbei în punctul dat, iar
este torsiunea curbei în punctul dat, iar 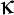 este curbura curbei în acelaşi punct.
este curbura curbei în acelaşi punct.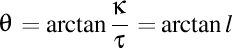 , iar modulul torsiunii complexe
, iar modulul torsiunii complexe 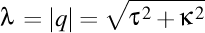 are şi el importanţa sa în Fizica elicoidală.
are şi el importanţa sa în Fizica elicoidală.