| | | |
 Home /
Home /
Formulele lui Frenet  Uploading .... Uploading ....
Formulele lui Frenet sunt relaţii matematice care stabilesc o legătură între versorii triedrului lui Frenet şi derivatele acestora.
Aceste formule pot fi scrise în forma geometrică, algebrică, trigonometrică şi exponenţială.
Fie 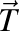 , , 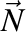 , , 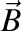 , versorii triedrului Frenet şi , versorii triedrului Frenet şi 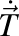 , , 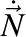 , , 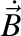 derivatele acestora în raport cu timpul, iar derivatele acestora în raport cu timpul, iar 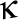 şi şi 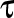 curbura şi torsiunea traiectoriei. curbura şi torsiunea traiectoriei.
Cu aceste notaţii, formulele lui Frenet pot fi scrise astfel (forma algebrică):
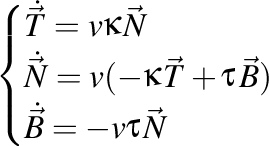 , ,
unde 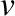 este viteza cu care se deplasează punctul material pe traiectoria respectivă. este viteza cu care se deplasează punctul material pe traiectoria respectivă.
Dacă notăm 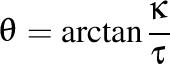 şi şi 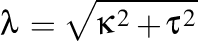 atunci avem atunci avem 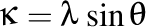 şi şi 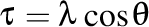 , iar formulele lui Frenet pot fi scrise în forma trigonometrică , iar formulele lui Frenet pot fi scrise în forma trigonometrică
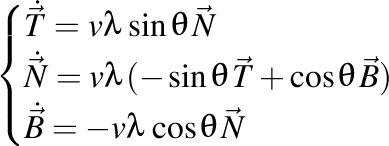 . .
Forma exponenţială a formulelor lui Frenet este dată de relaţiile:
 . .
Observaţi aici că versorul 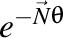 joacă un rol deosebit de important. joacă un rol deosebit de important.
În baza unei teoreme de recurenţă, formulele lui Frenet sunt recursive.
-(1205131034) În raport cu parametrul canonic formulele lui Frenet se pot scrie
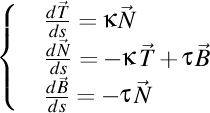 . .
Aşadar, avem 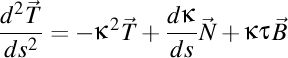 . .
Făcând calculele mai departe, avem
-(1205131126) Continuăm aceste calcule, făcând însă presupunerea că darbuzianul curbei date este unitar, adică 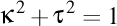 . .
În aceste condiţii,
Mai departe avem .
|
|
|
| | | |
|

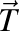 ,
, 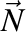 ,
, 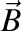 , versorii triedrului Frenet şi
, versorii triedrului Frenet şi 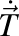 ,
, 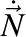 ,
, 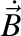 derivatele acestora în raport cu timpul, iar
derivatele acestora în raport cu timpul, iar 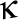 şi
şi 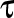 curbura şi torsiunea traiectoriei.
curbura şi torsiunea traiectoriei.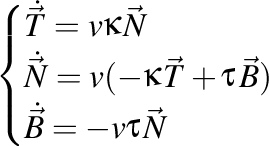 ,
,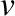 este viteza cu care se deplasează punctul material pe traiectoria respectivă.
este viteza cu care se deplasează punctul material pe traiectoria respectivă.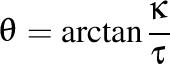 şi
şi 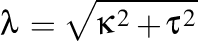 atunci avem
atunci avem 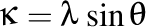 şi
şi 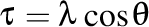 , iar formulele lui Frenet pot fi scrise în
, iar formulele lui Frenet pot fi scrise în 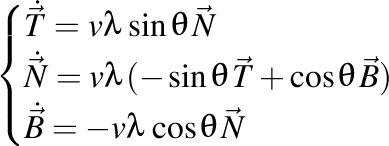 .
. .
.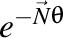 joacă un rol deosebit de important.
joacă un rol deosebit de important. 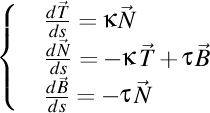 .
.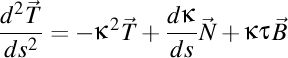 .
.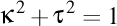 .
.