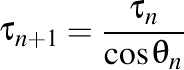| | | |
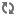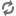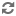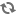 Uploading .... Uploading ....
Torsiunea este un parametru geometric al unei traiectorii care, împreună cu curbura, descrie complet traiectoria respectivă, fiind exprimarea cantitativă a vitezei cu care traiectoria se îndepărtează de planul osculator.
Dată fiind ecuaţia carteziană a unei curbe,
 , ,
valoarea torsiunii acestei curbe va fi
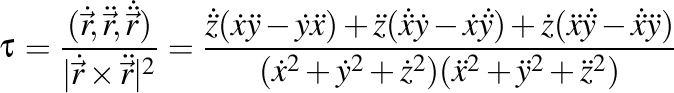 . .
Cunoscând că 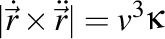 , mai rezultă că , mai rezultă că
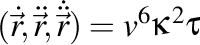 . .
(-(1103230916) Interesanţi exponenţii, egali cu factorii vitezei volumice, vitezei areolare şi vitezei liniare, respectiv.)
-(1205151427) Observaţi că produsul mixt are semnul torsiunii.
Observaţi că dacă produsul mixt de la numărător este nul, atunci şi torsiunea este nulă (şi reciproc). Dar produsul mixt este nul dacă şi numai dacă volumul format de cei trei vectori este nul, deci dacă şi numai dacă cei trei vectori sunt coplanari. Dar dacă cei trei vectori sunt coplanari, înseamnă că şi traiectoria este plană. Prin urmare, torsiunea unei traiectorii este nulă dacă şi numai dacă acea traiectorie este plană.
Torsiunea de ordinul n+1 este dată de formula
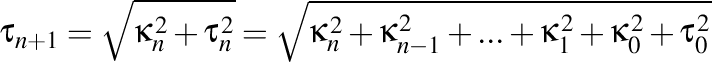 . .
Mai ştim că 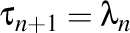 şi că şi că 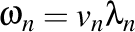 . De aici rezultă şi că . De aici rezultă şi că
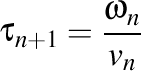 . .
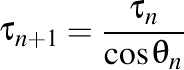
Există două tipuri de torsiuni: torsiunea totală şi torsiunea de ordin maxim (sau, mai bine, torsiunea finală).
O particulă care se deplasează rectiliniu are torsiune, iar această torsiune poate fi pusă în legătură cu spinul particulei.
Dată fiind curba x=x(t)=[x1(t),x2(t),x3(t)] în coordonate carteziene, torsiunea ei se poate calcula cu Maxima folosind funcţia
torsiune(x,t):=(diff(x[3],t,3)*(diff(x[1],t)*diff(x[2],t,2)-diff(x[2],t)*diff(x[1],t,2))
+diff(x[3],t,2)*(diff(x[1],t,3)*diff(x[2],t)-diff(x[1],t)*diff(x[2],t,3))+diff(x[3],t)*(diff(x[1],t,2)*diff(x[2],t,3)-diff(x[1],t,3)*diff(x[2],t,2)))/(((diff(x[1],t))^2+(diff(x[2],t))^2+(diff(x[3],t))^2)*((diff(x[1],t,2))^2+(diff(x[2],t,2))^2+(diff(x[3],t,2))^2));
Vezi şi torsiunea unei drepte.
-Ipoteze
-(1103230911) Torsiunea este curbură complexă. Curbura şi torsiunea ar putea constitui împreună un număr complex.
|
|
|
| | | |
|

 ,
, 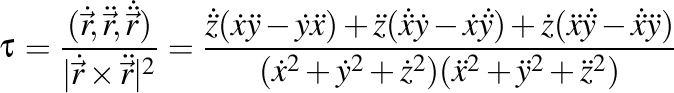 .
.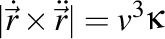 , mai rezultă că
, mai rezultă că 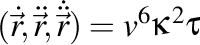 .
.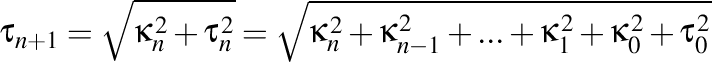 .
.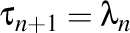 şi că
şi că 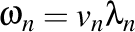 . De aici rezultă şi că
. De aici rezultă şi că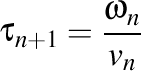 .
.