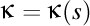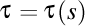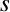Elicea închisă este o curbă de lancretian constant şi de lungime nenulă şi finită.
Pentru elicea închisă vectorul lui Darboux păstrează o direcţie constantă, dar modulul său variază după o funcţie periodică. Aşadar, cea mai simplă elice închisă este aceea pentru care darbuzianul este cea mai simplă funcţie periodică, adică o sinusoidă sau o cosinusoidă.
[Probleme]
-Vrem să determinăm lungimea elicei închise în funcţie de torsiunea şi lancretianul ei.
-Dacă cunoaştem ecuaţiile naturale ale elicei, atunci este suficient să inversăm funcţia care ne dă torsiunea în funcţie de parametrul natural.
-Ecuaţiile naturale ale unei elice sunt:
, unde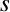 
este parametrul canonic. Putem spune că ecuaţiile naturale ale unei elice sunt date de o funcţie care asociază unui număr real un număr complex. .
-De asemenea, vrem să determinăm rolul analizei Fourier în studiul elicei închise.
[/Probleme]
[Ipoteze]
-Probabil, electronul este un luxon care se deplasează pe cea mai simplă elice închisă, al cărei darbuzian este o sinusoidă.
-Probabil, atomul de hidrogen este un ansamblu format de doi electroni defazaţi cu 90o, în care cel al cărui darbuzian este o cosinusoidă poate fi numit tocmai proton.
-Aşadar, probabil, protonul este un luxon care se deplasează pe o elice închisă al cărui darbuzian este o cosinusoidă.
-Probabil fotonul este un ansamblu de doi electroni cu torsiuni opuse şi aflaţi în fază, iar atomul de hidrogen este un ansamblu de doi electroni defazaţi. Pentru a clarifica aceste aspecte trebuie văzut cum se conservă impulsul şi momentul cinetic în aceste cazuri.
-Probabil, corpurile aflate în mişcare sunt elice deschise pe la capetele în care curbura şi torsiunea au valorile cele mai mici.
[/Ipoteze]
In English
The closed helix is a closed curve with constant lancretian and nonzero and finite length.
For closed helix, the Darboux vector maintains a constant direction, but a module varies as a periodic function. Therefore, the simplest closed helix is that for wich the darbuzian is the simplest periodic function, ie a sinusoid.
[Problems]
-We want to determine the length of the closed helix depending on her torsion and on her lancretian.
-Also, we want to determine the role of Fourier analysis in the study of closed helix .
[/ Problems]
[Assumptions]
-Probably, the electron is a luxon movind on the simplest closed helix, of which darbuzian is a sinusoid.
-Probably, the hydrogen atom is a compilation of two electrons shifted to 90°, the one whose darbuzian is a cosine can be called just proton.
-So, probably the proton is a luxon moving on a closed helix whose darbuzian is a cosine.
-Perhaps the photon is a set of two electrons with opposite torsion and are in phase and the hydrogen atom is a set of two electrons shifted. To clarify these issues should be seen as that momentum and angular momentum is conserved in these cases.
-Probably, the bodies are moving on helices open on the ends where the curvature and the torsion have the lowest values.
[/ Assumptions]
Uploading ....
