| | | |
 Home /
Home /
Théorème de recurrence 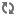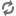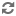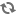 Uploading .... Uploading ....Etudier les formules de Frenet, J'en ai conclu que ils sont récursif. Plus précisément, à l'aide de forme trigonométrique de formules de Frenet, J'ai prouvé le suivant
Théorème: s'il ya un trièdre droit de n ordre 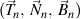
qui satisfait le formule de Frenet de n ordre, écrite comme la forme trigonométrique
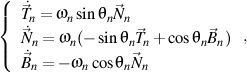
alors il ya un trièdre droit de n+1 ordre
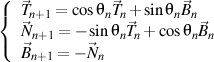
qui satisfait, à son tour, le formule de Frenet de n+1 ordre, écrite aussi comme la forme trigonométrique
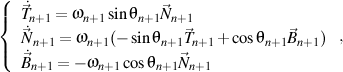
où
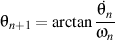 and and 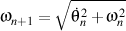
.
Démonstration :
Grâce à des relations 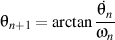 et et 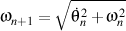
nous avons que
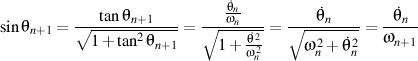
si
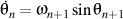
.
Nous avons également
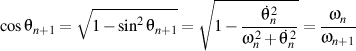
d'où
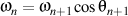
.
Maintenant, nous dérivons les vecteurs unitaires du trièdre de l'ordre n +1
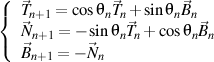
et nous obtenons
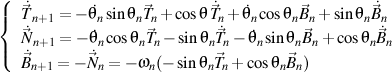
.
Remplacer
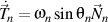
et
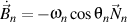
, nous obtenons
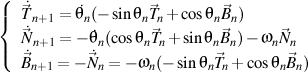
.
Mais, d'après de la définition des vecteurs unitaires de l'ordre de haut, nous savons que
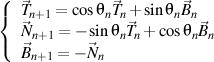
,
si
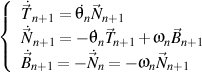
.
Parce que 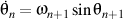 and and 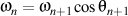 , ,
finalement abouti
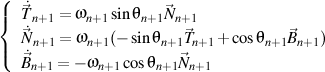
,
ce qui devrait être démontré.
|
|
|
| | | |
|

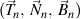
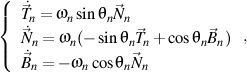
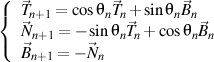
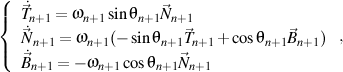
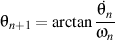 and
and 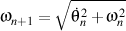
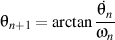 et
et 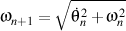
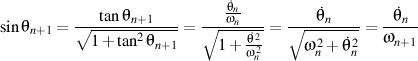
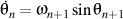
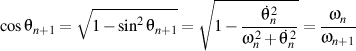
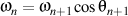
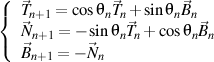
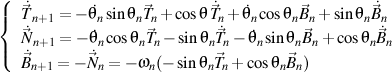
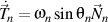
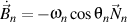
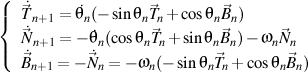
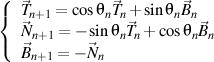
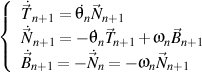
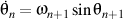 and
and 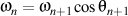 ,
,