| | | |
 Home /
Home /
Curbă spaţială  Uploading .... Uploading ....Numesc curbă spaţială acea curbă dată de ecuaţia carteziană parametrică
 , ,
unde  , ,  şi şi  sunt funcţii nenule şi indefinit derivabile care depind de un acelaşi parametru. sunt funcţii nenule şi indefinit derivabile care depind de un acelaşi parametru.
Oricărei curbe spaţiale i se poate asocia un triedru Frenet care se roteşte cu o viteză unghiulară a cărei direcţie şi al cărei modul nu sunt neapărat constante.
O curbă pentru care viteza unghiulară este constantă în direcţie se numeşte elice. Există şi curbe pentru care direcţia vitezei unghiulare nu este constantă, dar este constant modulul acesteia.
Curbura acestei curbe este
 , ,
iar torsiunea ei este
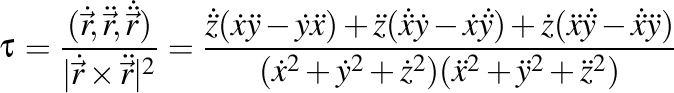 . .
Produsul vectorial dintre viteză şi acceleraţie (sau dintre impuls şi forţă) este coliniar cu binormala în punctul respectiv. Coeficientul de proporţionalitate dintre acest produs vectorial şi binormală este produsul dintre cubul modulului vitezei şi curbură.
Din punct de vedere matematic, dacă viteza şi acceleraţia sunt coliniare, atunci binormala rămâne nedefinită. În acest caz, numai proprietăţile fizice ale obiectelor mai pot permite convenţii privind direcţia binormalei.
Viteza unghiulară cu care se roteşte triedrul lui Frenet este dată de vectorul
 . .
Observaţi că viteza unghiulară este perpendiculară pe normală, neavând componente coliniare cu normala.
Pentru orice curbă spaţială avem relaţia
 . .
Datorită acestei relaţii, nu doar vectorul vitezei unghiulare este perpendicular pe normală, ci chiar şi vectorul derivatei vitezei unghiulare este perpendicular pe normală. Această proprietate remarcabilă a permis descoperirea triedrului complementar al lui Frenet şi, implicit, a teoremei de recurenţă a formulelor lui Frenet.
Derivata vitezei unghiulare poate fi scrisă astfel
 , ,
unde am notat  . .
Dacă raportul dintre curbură şi torsiune este constant, atunci chiar şi derivata a doua a vitezei unghiulare este perpendiculară pe normală.
Oricărei curbe spaţiale îi putem asocia o altă curbă spaţială, mai simplă, definită ca fiind curba a cărei tangentă este dată de versorul vitezei unghiulare a triedrului Frenet. Elicea este o curbă de ordinul unu pentru că acea curbă definită de viteza unghiulară este tocmai axa elicei, care este o dreaptă. Dreptele sunt curbe de ordinul zero deoarece curba descrisă de viteza unghiulară este identică cu curba însăşi. Prin recurenţă, rezultă că unei curbe îi putem asocia mai multe curbe din ce în ce mai simple, până când ajungem la o dreaptă.
Această recurenţă ne permite să susţinem că punctul care se deplasează pe curba spaţială este însoţit de un alt set de puncte care descriu simultan curbe din ce în ce mai simple asociate curbei iniţiale. Aşadar, putem redefini ordinul unei curbe ca fiind numărul de puncte (diferite de punctul de pe curbă) care pot fi asociate unui anumit punct de pe curba respectivă.
De exemplu, unui punct de pe elicea de mai jos

îi putem asocia originea normalei. Dar originea normalei se deplasează pe o dreaptă, deci alte puncte asociate nu mai putem găsi. Aşadar, elicea are ordinul unu (iar dreapta ordinul zero).
|
|
|
| | | |
|

 ,
,  ,
,  şi
şi  sunt funcţii nenule şi indefinit derivabile care depind de un acelaşi parametru.
sunt funcţii nenule şi indefinit derivabile care depind de un acelaşi parametru.
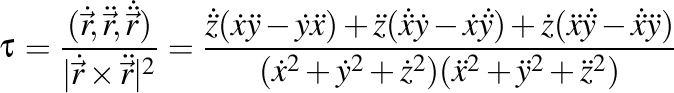 .
. .
. .
. ,
, .
.
