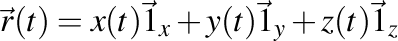Numesc lancretian acel
număr real asociat unei curbe dat de raportul dintre curbura
şi torsiunea acelei curbe.
Proprietăţi: Lancretianul curbei
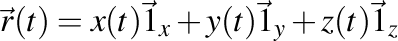
-1). Nu se
schimbă dacă facem o permutare circulară a funcţiilor din definiţia
curbei. Această proprietate denotă că lancretianul este invariant la
rotaţii ale reperului. De asemenea, dacă interschimbăm două funcţii, se
schimbă doar semnul lancretianului.
-2). Lancretianul nu se schimbă nici dacă
adunăm constante arbitrare la funcţiile ce definesc curba. Această
proprietate denotă că raportul este invariant la translaţii ale
reperului.
-3). Nu se schimbă nici dacă înmulţim toate funcţiile cu
acelaşi număr pozitiv. Această proprietate denotă că raportul este
invariant la dilatări ale reperului. Dacă numărul este negativ, atunci
raportul îşi schimbă doar semnul.
-4) (1103232113) În general, lancretianul nu se schimbă la o transformare conformă a reperului.
-5). Valoarea lancretianului
este dată de formula
.
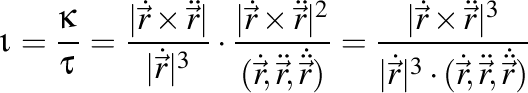Să notăm cu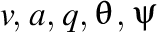 
respectiv modulul vitezei, al acceleraţiei, al supraacceleraţiei, unghiul dintre viteză şi acceleraţie şi unghiul dintre produsul vectorial dintre viteză şi acceleraţie şi supraacceleraţie. Atunci lancretianul se mai poate scrie
.
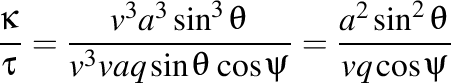Lancretianul este nul dacă modulul acceleraţiei este nul sau dacă viteza şi acceleraţia sunt coliniare sau dacă modulul vitezei sau al supraaceleraţiei este infinit, în timp ce restul valorilor rămân finite şi nenule. De aici rezultă, de exemplu, că un punct fizic cu acceleraţie finită are lancretianul nul.
Observaţie: denumirea noţiunii a fost aleasă având în vedere faptul că
importanţa raportului dintre curbură şi torsiune a fost scoasă în
evidenţă de teorema lui
Lancret. Evident, lancretianul traiectoriei este o noţiune extrem
de importantă a Fizicii viitorului, deci este importantă denumirea sa.
Cercetări
din Fizica
elicoidală sugerează că lancretianul deschide noi perspective
pentru înţelegerea sarcinii electrice a unui corp, invocând existenţa
unei legături profunde între cele două mărimi.
-(1006241404) Dacă
lancretianul unui sistem este nul, atunci sistemul se deplasează
rectiliniu. În acest caz, singurul parametru variabil al sistemului este
torsiunea.
[Întrebări]
-(1009081625) Dacă lancretianul este constant, atunci traiectoria este deschisă? (1103112126) Dacă lancretianul este constant, atunci corpul se mişcă pe o elice. Rămâne de văzut dacă există elice închise. Oare există elice închise?
-(1205061041) Da, există elice închise. De exemplu, cele pentru care modulul vectorului lui Darboux este o funcţie sinusoidală, în timp ce lancretianul este constant.
[/Întrebări]
-(1010172221) Având în vedere faptul că oricărui vector i se poate asocia un triedru Frenet, rezultă că oricărui vector i se poate calcula un lancretian.
-(1103111953) Putem vorbi de lancretian de ordinul n ca fiind raportul dintre curbura de ordinul n şi torsiunea de ordinul n.
-(1201102256) Drepte, curbele plane şi elicele au curbura de ordinul 2 nulă.
[Ipoteze]
-(1103112009) Corpurile se mişcă în aşa fel încât lancretianul lor să fie cât mai aproape de unitate. Au tendinţa de a avea un lancretian egal cu unitatea. Sau o fi un multiplu întreg de unităţi?
-(1205090935) Lancretianul este sarcină electrică. Deci, lancretianul se cuantifică. Deci variaţiile lancretianului nu sunt continue, ci în salturi.
-(1205090938) Am putea presupune că orice curbă este cunoscută dacă îi cunoaştem lancretianul în fiecare punct. Ba, mai mult, putem presupune că există o corespondenţă biunivocă între orice curbă şi lancretianul ei. Asta dacă admitem că vorbim doar despre curbele închise care pornesc din şi ajung în origine. Aşadar, dacă cunoaştem o funcţie reală de o variabilă reală (care asociază oricărui parametru scalar independent tocmai lancretianul), atunci cunoaştem curba din spaţiu asociată lancretianului respectiv.
[/Ipoteze]
-
-
Uploading ....