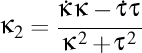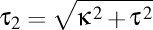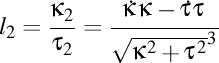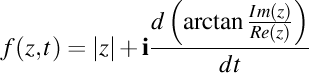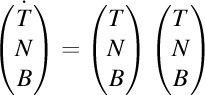| | | |
 Uploading .... Uploading ....Această pagină conţine încercările mele haotice prin care voi căuta să ajung la concluzii adevărate şi profunde. Ea este din păcate foarte variabilă şi uneori incomprehensibilă. Voi face eforturi continue de clarificare a ei, dacă nu pentru mine, măcar pentru cititori. Câteva dintre gândurile exprimate aici pot face obiectul unor articole de sine stătătoare. Asta mai înseamnă că pe măsură ce se adună text va trebui să îl duc în altă parte.
-Ordine între ideile adevărate şi între întrebări.
-Cum se mişcă baricentrul.
-Inerţia la dilatare.
-Ce trebuie să conţină în plus lagrangeanul pentru a fi mai realist, pentru a ţine seama şi de impulsul volumic.
-Legătura mişcărilor cu fractalii.
-Tendinţa de uniformizare a temperaturilor, a energiilor şi legătura acestei tendinţe cu existenţa câmpurilor din vecinătatea sistemelor.
-Rolul liniilor de câmp magnetic pentru mişcare.
-Este adevărat oare că toate corpurile urmează liniile de câmp magnetic pe care le pot urma? Adică, corpurile mai grele urmează numai linii de câmp magnetic mai simple, iar corpurile mai uşoare pot urma numai liniile de câmp magnetic mai întortocheate. Masa corpurilor este în legătură strictă cu complexitatea liniilor de câmp magnetic în care se află.
-(1006280842) Oare corpurile urmează liniile de câmp magnetic sau se înfăşoară în jurul lor? Cred mai degrabă că se înfăşoară.
-(1006252253) Orice corp în rotaţie (sau precesie) este
un magnet. Orice corp în mişcare este un curent electric.
-(1006252303) Impulsul există datorită translaţiei, iar momentul cinetic există datorită rotaţiei.
-(1006280854) Orice linie de câmp magnetic este un curent electric de deplasare şi, reciproc, orice curent electric de deplasare este o linie de câmp magnetic.
-(1007142353) De ce se atrag corpurile? Cum intervine legea de conservare pentru a impune o asemenea atracţie? Vezi legătura cu uniformizarea temperaturilor.
-(1012111636) Poziția unui punct material de masă m este  . Atunci avem . Atunci avem  , unde , unde  . .  . Dar . Dar  , unde , unde  , este triedrul lui Frenet asociat poziției. , este triedrul lui Frenet asociat poziției.
-(1101042114) Pornim de la un sistem finit de puncte materiale. Ne interesează mişcarea baricentrelor sale, energiile implicate, restricţiile care se impun într-o asemenea mişcare. În ce măsură elicele de mişcare au curbura egală cu torsiunea? Ce câmpuri apar dacă această condiţie nu este îndeplinită?
-(1101042119) Probabil, torsiunea tinde să se anuleze. Atunci ar exista două tipuri de tendinţe de anulare a torsiunii, una care să mărească raportul dintre curbură şi torsiune (lancretianul), iar cealaltă care să micşoreze lancretianul. Tendinţa de mărire a lancretianului s-ar manifesta ca o atracţie, iar tendinţa de micşorare a lancretianului s-ar manifesta ca o respingere. Probabil că tendinţa de anulare a torsiunii are efecte electromagnetice. Mai precis, în absenţa câmpurilor electromagnetice, torsiunea este instantaneu nulă. Asta înseamnă că valoarea torsiunii ne spune totul despre câmpul care o produce.
-(1101042125) Dar nu doar torsiunea trebuie să tindă să se anuleze, ci şi curbura. În absenţa câmpurilor (gravitaţionale?), curbura este instantaneu nulă. Asta înseamnă că valoarea curburii spune totul despre câmpul care o produce.
-(1101042144) Înseamnă că într-un sistem liber de particule, curbura totală şi torsiunea totală trebuie să fie nule. Trebuie văzut ce înseamnă curbură totală şi torsiune totală. Oare curbura totală este suma curburilor, iar torsiunea totală este suma torsiunilor?
-(1101042147) Probabil, un corp cu torsiunea mai mare decât curbura este încărcat electric opus faţă de un corp cu torsiunea mai mică decât curbura. Asta ar putea însemna că un corp este neutru din punct de vedere electric dacă torsiunea este strict egală cu curbura. Altfel spus, corpurile sunt încărcate electric într-un sens dacă lancretianul lor este supraunitar şi sunt încărcate electric în sens opus dacă lancretianul lor este subunitar, în valoare absolută. Semnul lancretianului ne dă probabil distincţia dintre materie şi antimaterie.
-(1101042159) Atât curbura, cât şi torsiunea pot fi anulate ambele prin mărirea la infinit a pasului elicei tangente. Înseamnă că tendinţa generală de mişcare va fi ca pasul elicei tangente să crească necontenit. Următoarea tendinţă va fi ca raza elicei tangente să devină egală cu pasul ei. Prin aceasta, în mişcarea sa, corpul va fi însoţit de două tendinţe, una de mărire a pasului şi alta de menţinere a razei egală cu pasul.
-(1101070757) Observăm că formula curburii elicei este foarte asemănătoare cu formula torsiunii elicei, iar asta poate însemna că nici curbura şi nici torsiunea nu au importanţă fundamentală de sine stătătoare, ci doar o combinaţie a lor, precum este lancretianul sau radicalul din suma pătratelor lor.
-(1101070803) Putem interpreta acceleraţia într-un mod caracteristic Fizicii elicoidale, uzând de proprietăţile interesante ale curburii şi torsiunii. Dacă viteza unui corp creşte, înseamnă că creşte pasul elicei tangente, deci lancretianul scade, iar dacă viteza corpului scade, pasul elicei tangente scade, ceea ce înseamnă că lancretianul creşte.
-(1101070827) Din aceste raţionamente privitoare la lancretian ies în evidenţă trei valori foarte importante ale acestuia: valoarea nulă, unitatea şi valoarea infinită. Valoarea nulă pentru lancretian corespunde mişcării cu viteza maximă pe o traiectorie rectilinie. În acest caz, pasul elicei tangente este infinit sau raza elicei tangente este nulă.
-(1103131612) Mă gândesc că dacă orice mişcare este compusă din translaţii, atunci aş putea demonstra cumva mai direct că există inerţie la precesie. Dacă aş putea arăta că inerţia la rotaţie provine din inerţia la translaţie, atunci aş putea arăta şi că inerţia la precesie provine din inerţia la rotaţie. Aş putea folosi şi conservarea distanţei parcurse în unitatea de timp, a ariei parcurse în unitatea de timp şi a volumului parcurs în unitatea de timp. Dealtfel, chiar asta am şi folosit în deducerea teoretică.
-(1103131641) Să presupunem că un punct material de masă constantă se deplasează cu o viteză liniară constantă. În acest caz, există o dreaptă unică şi fixă în Univers pe care se deplasează punctul material. Fiind unică şi fixă, putem numi această dreaptă tocmai dreapta de mişcare. Mai mult, punctul material străbate distanţe egale în unităţi de timp egale pe dreapta de mişcare. Dacă fixăm un punct pe dreapta de mişcare, putem construi o funcţie care asociază fiecărui moment de timp lungimea segmentului dintre cele două puncte. Numim acest punct (arbitrar ales) pol liniar. Pentru orice alt pol liniar ales pe dreapta de mişcare, funcţia asociată diferă doar printr-o constantă. Aşadar, derivata în raport cu timpul a acestei funcţii nu mai depinde de polul liniar ales.
-(1103131715) Dacă, pe lângă polul liniar ales, mai alegem un punct din exteriorul dreptei de mişcare, punct pe care îl numim pol areolar, atunci mai putem construi o funcţie care asociază fiecărui moment de timp aria triunghiului format de cele trei puncte.
-(1103131732) Sau am putea vorbi de lungimea unei curbe, de aria ei şi de volumul curbei. Lungimea curbei se măsoară faţă de un punct al curbei. Aria curbei se măsoară faţă de un punct din afara curbei, aflat în planul ei osculator. Volumul curbei se măsoară faţă de un punct din afara planului osculator. Pentru a defini lungimea avem nevoie de două puncte foarte apropiate. Pentru a defini aria avem nevoie de trei puncte foarte apropiate. Pentru a defini volumul avem nevoie de patru puncte foarte apropiate.
-(1103131752) Dată fiind o curbă şi un punct material care se mişcă pe acea curbă, se pot defini viteza liniară, viteza areolară şi viteza volumică pentru punctul material respectiv.
-(1103141722) Avem


de unde mai rezultă şi faptul că

-(1103221320) Dacă transformările conforme nu modifică unghiul dintre două curbe, înseamnă că două elice nu diferă una de cealaltă decât printr-o transformare conformă. Altfel spus, transformările conforme nu modifică lancretianul unei elice şi nici ordinul ei.
-(1104191946) Vreau să fac o legătură între contracţia relativistă şi proprietăţile elicei şi ale unei bobine. Dacă o elice (bobină) are o anumită rază şi un anumit pas pentru observatorul în repaus, atunci pentru un observator care se mişcă faţă de elice paralel cu axa acesteia, pasul va apărea mai mic. Pin urmare, lancretianul elicei va apărea mai mare
-(1108060724) Ştim că viteza unghiulară este perpendiculară pe normală şi că, de asemenea, chiar şi derivata vitezei unghiulare este perpendiculară pe normală.
-(1108092128) Vreau să-mi reamintesc cât este proiecţia vitezei pe axa elicei circulare, în funcţie de raza şi pasul elicei. Dacă notăm cu 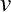 viteza pe elice şi cu viteza pe elice şi cu 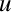 proiecţia acestei viteze pe axă, atunci trebuie să avem relaţiile proiecţia acestei viteze pe axă, atunci trebuie să avem relaţiile 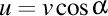 , unde , unde 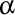 este unghiul dintre tangenta la traiectorie şi axa elicei, deci şi unghiul dintre tangentă şi vectorul lui Darboux. Aşadar, avem mai exact este unghiul dintre tangenta la traiectorie şi axa elicei, deci şi unghiul dintre tangentă şi vectorul lui Darboux. Aşadar, avem mai exact 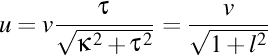 , unde , unde 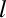 este raportul dintre curbură şi torsiune, adică lancretianul elicei. este raportul dintre curbură şi torsiune, adică lancretianul elicei.
-Deci, proiecţia vitezei depinde doar de lancretianul elicei, nu şi de curbura elicei sau torsiunea ei luate separat. Asta mai înseamnă şi că viteza aparentă a unui corp care merge pe o elice nu depinde de modul în care variază parametrii elicei, din moment ce axa elicei rămâne constantă. Prin urmare, dacă măsurăm doar proiecţia vitezei unui corp pe o elice, atunci nu vom putea trage concluzii despre modul în care variază parametrii elicei. Deci, indiferent că numărul de spire ale elicei este mai mare sau mai mic, proiecţia vitezei pe axa elicei depinde doar de viteza pe elice.
-(1108110805) Deci, măsurând viteza de-a lungul axei elicei, nu putem trage concluzii despre densitatea spirelor elicei. Atunci densitatea spirelor are legătură cu un alt parametru, probabil cu masa. Am putea spune că o densitate mai mare a spirelor echivalează cu o masă mai mare. Poate că proporţionalitatea este dată de constanta lui Planck. Şi îndrăznesc să presupun că densitatea variabilă implică apariţia sarcinii electrice, deşi e posibil ca sarcina electrică opusă să conste într-un lancretian opus (dar asta nu contravine ipotezei că sarcina ar fi variaţia densităţii spirelor).
-Oricum, densitatea spirelor poate fi variabilă chiar dacă este vorba despre mişcarea pe o elice. Deci, nu doar densitatea spirelor trebuie asociată unui parametru al sistemului (în acest caz, masei), ci şi variaţia densităţii spirelor trebuie asociată vreunui parametru al sistemului (deci, probabil, sarcinii electrice). Asta explică presupusa eventualitate ca fotonul să fie alcătuit din două corpuri care se mişcă pe câte o elice cu aceeaşi densitate a spirelor şi cu aceeaşi variaţie a densităţii spirelor, doar cu lancretian opus ca semn.
-Totuşi, nu cumva semnul lancretianului ne spune dacă este vorba de materie sau antimaterie (şi nu despre semnul sarcinii electrice)? O fi vreo diferenţă fundamentală între materialitate (materie sau antimaterie) şi sarcina electrică (pozitivă sau negativă)? Fizica actuală zice că da, este o diferenţă. Care o fi diferenţa din punctul de vedere al mişcării pe traiectorie? În plus, oare n-am putea răspunde acum la întrebarea privind cuantificarea sarcinii electrice? Nu cumva sarcina electrică se cuantifică tocmai pentru că nu au sens jumătăţile de spiră?
-(1108110922) Bun, deci trebuie clarificat ce este sarcina electrică şi masa din punctul de vedere al mişcării pe traiectorie. Există posibilitatea ca masa să fie densitatea de spire, iar sarcina electrică să fie variaţia densităţii de spire, pe de o parte, iar pe de altă parte, există posibilitatea inversă, aceea de a presupune că masa este variaţia de densitate şi că sarcina este densitatea spirelor.
-Dacă am presupune prima variantă, aceea în care masa este densitatea spirelor, iar sarcina este variaţia densităţii spirelor, atunci ar fi posibil să existe corpuri cu masă nenulă, dar neutre, fără sarcină electrică;
-Dacă am presupune că sarcina electrică este densitate de spire şi că masa este variaţie de densitate de spire, atunci ar putea exista corpuri încărcate electric dar care să nu aibă masă, ceea ce este oarecum inacceptabil, căci un corp încărcat electric ar trebui să aibă energie, deci şi masă.
-Ultima observaţie ne sugerează să aducem şi energia în discuţie, apoi să legăm energia de masă. Deci, parcă e mai clar că un corp cu densitate de spire are energie, aspect care ne încurajează să considerăm valabilă prima variantă, aceea în care masa este densitate de spire.
-Dar nu trebuie să uităm să tratăm relativist problema, în sensul de a ţine seama de modul în care depinde de observator densitatea de spire. Chiar, cum depinde de observator densitatea de spire? Din punct de vedere geometric ar trebui ca densitatea de spire să crească cu viteza, căci acelaşi număr de spire ale elicei se constată într-un interval spaţial contractat. Dar din punct de vedere cinematic trebuie să ţinem seama şi de faptul că viteza unghiulară se micşorează în funcţie de viteză. Nişte relaţii matematice ar fi binevenite aici.
-Mai avem de analizat şi problema modului în care poate varia densitatea spirelor. Cât de variabilă poate fi densitatea spirelor şi cum poate ea varia, oricum?
-(1108092322) Această constatare ne spune că dacă fotonul ar fi un ansamblu de (două) corpuri ce se deplasează pe o elice, atunci intrarea fotonului într-un anumit mediu obişnuit (prceum sticla) ar modifica doar viteza pe elice a fotonului, fără să modifice curbura sau torsiunea elicei. Ar mai însemna că unghiul de incidenţă la intrarea în mediul respectiv modifică lancretianul (căci direcţia nu se poate modifica cu un lancretian constant). Deci, la intrarea în mediu sub un anumit unghi se modifică numai unul dintre parametrii elicei. Asta înseamnă că unul dintre parametrii elicei pentru fotonul care a pătruns în mediu sub un anumit unghi de incidenţă are altă valoare decât avea când fotonul se afla în afara mediului.
-(1108092341) Dacă am face această analogie, atunci ar trebui să admitem că în vid curbura este nulă (torsiunea nu poate fi infinită, căci frecvenţa (care este proporţională cu radicalul sumei pătratelor dintre curbură şi torsiune) este finită), căci lancretianul ar trebui să fie nul (căci proiecţia vitezei pe axa elicei trebuie să aibă aceeaşi valoare cu viteza pe elice, adică viteza luminii în vid). Atunci, înseamnă că pătrunderea fotonului în mediu duce la creşterea razei elicei acestuia.
-
-(1108171434) Inerţia la precesie, inerţia la nutaţie, inerţia la...
După o lungă perioadă în care am fost destul confuz cu privire toate modurile posibile în care se poate mişca un corp solid cu un punct fix, am ajuns, în sfârşit, la concluzia că mişcările acestuia nu se limitează doar la precesie şi nutaţie
-Existenţa a numai trei unghiuri ale lui Euler (unghiul de rotaţie, unghiul de precesie şi unghiul de nutaţie) lasă impresia că singurele mişcări fundamentale ale solidului cu un punct fix ar fi rotaţia, precesia şi nutaţia. Dar aşa să fie oare? Oare dacă precesia este asociată cu variaţia rotaţiei, iar nutaţia este asociată cu variaţia precesiei, nu cumva există şi mişcări asociate tocmai cu variaţia nutaţiei? Şi aşa mai departe?
Ridic această problemă deoarece ea are o legătură cu consecinţele teoremei de recurenţă a formulelor lui Frenet, în special cu consecinţa dată de faptul că pentru orice traiectorie posibilă (fizică) există o dreaptă unică asociată acelei traiectorii, iar traiectoria este înfăşurată în jurul acelei drepte sub forma unor elice în jurul altor elice, numărul acestor elice depinzând de modul de variaţie a parametrilor instrinseci ai traiectoriei.
Să concretizăm puţin la ce mă refer când vorbesc despre această legătură. Să presupunem că un corp solid se deplasează rectiliniu fără rotaţie. În acest caz, toate particulele sale descriu drepte. Apoi, dacă intervine o cauză oarecare, corpul solid începe să se şi rotească. Rotaţia solidului face ca particulele sale să descrie elice. Dacă, mai departe, este tulburată şi această mişcare de rotaţie a solidului, producându-i-se acestuia şi o precesie, atunci particulele solidului încep să descrie o traiectorie cu un ordin mai complicată decât o elice, adică încep să descrie aşa numitele „curbe de precesie constantă”. Mai departe, nutaţiei ar trebui să îi corespundă „curbe de nutaţie constantă” (dar nu ştiu să existe aşa ceva în literatura de specialitate). Şi cum nu văd nicio limitare în a merge mai departe cu asemenea consideraţii, rezultă că nu ar trebui să existe limite nici în ceea ce priveşte numărul posibil de mişcări pe care le poate avea un corp solid cu punct fix, dincolo de precesie şi de nutaţie.
-(1109162125) Mă gândesc la un fel de ierarhizare a curbelor din spaţiu.
-Derivata unei curbe ar putea fi o curbă de ordin inferior, iar integrala unei curbe ar putea fi o curbă de ordin superior. Am putea reprezenta grafic lancretianul în funcţie de timp. Am putea spune că unei drepte i-ar corespunde o paralelă la axa absciselor, iar unei elice i-ar corespunde ecuaţia unei drepte. Sau am putea să facem un grafic bidimensional cu valoarea torsiunii în funcţie de curbură. Curbura ar putea fi pe axa ordonatelor, iar torsiunea pe axa absciselor.
-Mergând pe această linie, derivata unei elice ar fi o dreaptă, iar integrala unei drepte ar fi o elice.
-(1109162132) Mă mai gândesc să analizez şi radicalul, ca să văd dacă are proprietăţi asemănătoare lancretianului. Dacă da, atunci ar putea fi folosit alături de lancretian pentru a defini un nou aparat matematic ce ar opera cu aceste două elemente în locul curburii şi torsiunii. Ar trebui să scriu un articol cu proprietăţile lancretianului şi ale radicalului. Ia să începem.
-Presupunând că cititorul cunoaşte noţiunile de curbură şi torsiune ale unei curbe din spaţiu, vom prezenta aici proprietăţile a două alte noţiuni importante
-(1110301110) Important: ciocnirea care nu modifică direcţia impulsurilor conservă momentele cinetice. Şi reciproc. De asemenea, ciocnirea care nu modifică direcţiile momentelor cinetice conservă impulsurile volumice. Şi reciproc.
-(1202260006) Vrem să construim nişte numere complexe relaţionate. Fie un număr complex 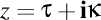 , scris sub formă trigonometrică , scris sub formă trigonometrică 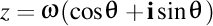 şi construim funcţia numită „derivata Frenet a unui număr complex în raport cu parametrul s” dată prin şi construim funcţia numită „derivata Frenet a unui număr complex în raport cu parametrul s” dată prin 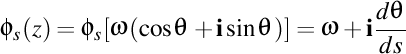 . Această funcţie poate fi aplicată de mai multe ori. . Această funcţie poate fi aplicată de mai multe ori.
-(1202260046) Nu merge aşa. Trebuie folosite particular pentru vectorii lui Darboux. Primul vector Darboux este 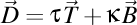 , iar vectorul Darboux de ordinul doi este , iar vectorul Darboux de ordinul doi este 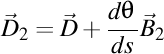 . Deci, . Deci, 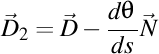 . Putem scrie atunci că . Putem scrie atunci că 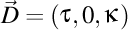 , iar , iar 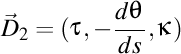 . . 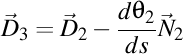 . .
-(1202261252) Mai putem scrie atunci în forma trigonometrică faptul că 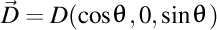 , , 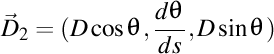 şi şi 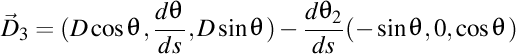 . .
-(1203051110) Un câmp gravitaţional produs de un corp îndepărtat poate fi considerat uniform. S-ar părea că putem considera că într-un asemenea câmp corpurile se deplasează rectiliniu (sau circular?).
-(1203051115) Am avea de calculat dacă nu cumva forţa care menţine corpul pe orbita elicoidală este tocmai forţa gravitaţională.
-(1203261903) Am de inventat un formalism matematic necesar unei exprimări riguroase în domeniul Fizicii elicoidale. Trebuie să inventez nişte simboluri cu care pot opera şi din care să rezulte proprietăţile pe care le au corpurile la care se referă simbolurile. De exemplu, trebuie să inventez un simbol care să-mi arate că este vorba de două corpuri ce aparţin unui sistem cu impulsul conservat care corpuri se deplasează pe o elice de o anumită curbură şi torsiune. Dintr-o asemenea simbolistică trebuie să-mi rezulte, de exemplu, că impulsul total se poate conserva şi dacă cele două corpuri ale sistemului nu se deplasează într-un plan perpendicular pe impulsul total (şi de află, însă, coliniar cu centrul de masă).
-S-ar părea că un asemenea aparat matematic lucrează cu baricentre.
-Trebuie văzut ce operaţii se pot realiza cu baricentrele. De exemplu, mă gândesc la noţiunea de „diviziune a unui baricentru”. Sau s-o numesc „fisiune”, ca să fie loc şi pentru „fuziune”?
-În orice sistem există un baricentru principal a cărui traiectorie este o dreaptă şi care nu poate fi tulburată prin mijloace interne sistemului. El se stabileşte prin convenţie şi îl vom numi baricentru de ordinul zero sau baricentrul principal. El coincide cu centrul de masă al sistemului.
-(1204012003) Dacă traiectoria unui corp faţă de un anumit reper este o linie dreaptă, atunci faţă de un alt reper care complică traiectoria doar cu un ordin, traiectoria trebuie să fie o elice (de ordinul 1).
-Trebuie să găsesc legătura între ordinul curbelor şi ordinul derivatei lancretianului.
-(1204250947) Dacă avem o oarecare viteză de rotaţie, atunci trebuie să admitem că avem şi o viteză de translaţie. Şi reciproc.
-(1204281127) Un vector constant. Un sistem fizic aflat în vid poate fi interpretat ca fiind un câmp vectorial de impulsuri, de momente cinetice şi de impulsuri volumice, cu proprietatea că impulsul său total, momentul său cinetic total şi impulsul volumic total al sistemului se conservă (sunt constante). Dacă ultimele variază, atunci sistemul considerat nu este în vid, ci este într-un câmp produs de un alt sistem aflat în vecinătate.
-(1204281143) Un câmp electromagnetic se deplasează în toate direcţiile şi este caracterizat de doi parametri: frecvenţă şi amplitudine. Vrem să încercăm o analogie cu o familie de curbe care trec printr-un punct comun şi sunt caracterizate tot de doi parametri: curbură şi torsiune. Atunci am putea asocia unei radiaţii monocromatice o elice.
-(1204281156) De ce nu cad stelele? Pentru că ele fac parte dintr-un sistem mai mare în raport cu care ele cad spre centrul acelui sistem. Un răspuns analog se poate da şi pentru a explica stabilitatea materialelor.
-(1205060950) Dacă torsiunea şi curbura nu depinde de rotaţia reperului sau de translaţia acestuia, atunci ar trebui ca parametrii ce importă în studiul curbelor să nu depindă nici de dilatarea reperului. Astfel am ajunge să putem identifica o curbă nu cu doi parametri, ci chiar cu unul singur, acesta fiind tocmai lancretianul (care nu se modifică nici măcar la o dilatare a reperului).
-(1205061044) Mă gândesc să introduc şi noţiunea de „darbuzian” ca fiind tocmai modulul vectorului lui Darboux.
-(1205090949) Mulţimea curbelor închise care trec prin origine reprezintă o mulţime importantă. Probabil, ea este izomorfă cu mulţimea funcţiilor reale de o variabilă reală.
-(1205211354) Vreau să determin curbura şi torsiunea unei curbe închise şi continue (Jordan). Pentru aceasta trebuie să pornesc de la faptul că o curbă închisă şi continuă are coordonate periodice şi continue, deci este o serie Fourier.
-(1206080832) Vreau să determin ecuaţia generală a unei elice. Am găsit că orice curbă poate fi scrisă ca (x(t), y(t), t) unde t este parametrul independent. Să vedem cât o fi curbura şi torsiunea acestor curbe. De asemenea, să vedem cât este x şi y atunci când cunoaştem lancretianul.
-(1206121231) Perechi de numere. Mă gândesc că s-ar putea ca între lungimea unei curbe şi curbura şi torsiunea ei să existe o corespondenţă biunivocă, chiar dacă unul este un scalar şi „celălalt” este o pereche de numere. Aceasta pentru că mă gândesc la ceva asemănător cu faptul că unui număr raţional îi putem asocia o pereche de numere întregi, iar unui număr real am putea să-i asociem atunci o pereche de numere raţionale din care să facem un număr complex. Şi poate că atunci ar rezulta şi faptul că torsiunea complexă este o pereche de numere raţionale.
-Problema este că unui număr raţional îi putem asocia chiar un singur număr întreg, nu neapărat două, căci mulţimea numerelor raţionale este şi ea numărabilă. Aşadar, unui număr real nu-i putem asocia în mod biunivoc o pereche de numere raţionale pentru că mulţimea numerelor reale este nenumărabilă.
-
-Să presupunem că elicea închisă ar avea torsiunea periodică. Să vedem dacă torsiunea periodică este suficientă pentru a închide o elice.
Care este condiţia ca o curbă Jordan să fie închisă?
Există o corespondenţă biunivocă între parametru şi lungimea curbei. Atunci nu cumva lungimea este chiar o funcţie periodică de parametru?
Nu cumva putem alege ca parametru tocmai lungimea segmentului descris de proiecţia curbei pe axa ei?
- Curbele închise au atât darbuzianul periodic, cât şi lancretianul.
- Modelarea realităţii
- Curbele sunt funcții care asociază unui număr real un număr complex. Și există posibilitatea să considerăm că ele sunt funcții care asociază unui număr real un lancretian.
- Așa cum orice număr complex este suma dintre un număr real pur și un număr imaginar pur, tot astfel, și o curbă este suma a două tipuri generale de curbe: curbe de curbură nulă și curbe de torsiune nulă.
- Se pare că asta este echivalent cu faptul că un câmp vectorial se descompune și el în două câmpuri, unul solenoidal (deci cu divergența nulă) și altul irotațional (deci cu rotorul nul).
- Ar trebui arătat că o asemenea curbă este închisă doar dacă fiecare componentă a sa este periodică și are aceeași perioadă.
-(1207271944) Am de studiat în două direcţii: direcţia mecanică şi direcţia electromagnetică. În direcţia mecanică storc tot ce se ştie privind mişcarea mecanică şi coroborez cu teorema de recurenţă, iar în direcţia electromagnetică aplic teorema de recurenţă liniilor de câmp electromagnetic. -În direcţia mecanică. Ştim că un corp liber are energia (masa), impulsul şi momentul cinetic constante. Dacă una dintre ele variază, înseamnă că acel corp nu este liber, ci este sub influenţa unui alt corp.
-Să vedem cum e cu energia. Energia este un scalar. A avea energie înseamnă a avea capacitatea de a interacţiona cu orice corp. Dacă un corp nu ar avea energie, atunci el nu ar avea nici masă. Dacă nu ar avea masă, atunci nu ar avea nici impuls şi nici moment cinetic. Aşadar, a avea energie este fundamental pentru interacţiuni. Să presupunem atunci aici că singurul parametru prin intermediul căruia interacţionează două sisteme este energia. Care vor fi consecinţele? A interacţiona prin energie înseamnă a face un transfer de energie de la un corp la altul. Cum poate un corp să transfere energie altui corp aflat în alt loc, la distanţă? Hmmm... Numai prin radiaţie! Radiaţia are loc într-o anumită direcţie. Corpul care cedează energie tinde să se îndepărteze de corpul care primeşte energie, iar corpul care primeşte energie tinde să se apropie de corpul care cedează energie. De ce o fi aşa? Pentru că corpul care cedează pierde masă, iar corpul care primeşte energie primeşte şi masă. Acesta este mecanismul care încetineşte sondele Pioneer!
-(1207290850) Transferul de masă. Transferul de impuls. Transferul de moment cinetic.
- Transferul de masă. Căldură, câmp electric. Transfer de viteză.
- Transferul de impuls. Câmp gravitaţional. Transfer de curbură.
- Să analizăm posibilitatea ca un câmp gravitaţional să atribuie (doar) curbura traiectoriei. Pentru corpurile care se rotesc în jurul planetei este clar de ce şi cum se atribuie curbura. Cum interpretăm ca fiind transfer de curbură faptul că vedem doar acceleraţie (deci transfer de viteză) la corpurile care cad spre centrul planetei?
- Oricum, câmpul gravitaţional se naşte datorită variaţiilor de impuls. Dacă variază numai direcţia impulsului, atunci nu apar variaţii de modul de impuls, deci nu apar variaţii de energie, deci nu apare câmp electric.
- Transferul de moment cinetic. Câmp magnetic. Probabil, variaţie de câmp gravitaţional, deci câmp gravitaţional variabil. Transfer de torsiune.
- Studiul potenţialului vector şi al celui scalar.
-(1208150858) Fractali elicoidali. Funcţie. Dacă 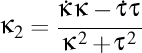 şi şi 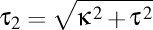 , atunci , atunci 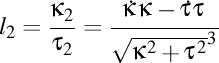 . . Deci, 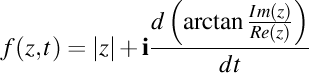 . . -(1210091349) Pentru a determina elementele traiectoriei avem nevoie de puncte. Dacă determinăm un singur punct, atunci cunoaştem poziţia.
-Dacă determinăm două puncte, atunci cunoaştem viteza liniară, lungimea parcursă în unitatea de timp, prima derivată a poziţiei, tangenta la traiectorie, direcţia mişcării. -Dacă determinăm trei puncte, atunci cunoaştem a doua derivată a poziţiei, acceleraţia, planul mişcării, viteza areolară, aria parcursă în unitatea de timp. -Dar ne ajunge să determinăm doar primele trei puncte pentru a cunoaşte cu precizie o traiectorie? Dacă nu, atunci câte puncte ne trebuie pentru aceasta? Oare patru sunt suficiente? Cinci? Şase? Un milion? Desigur, ideal ar fi să putem cunoaşte toate punctele traiectoriei şi abia atunci am putea spune că noi cunoaştem cu precizie acea traiectorie. Dar, cum nu putem cunoaşte toate punctele unei traiectorii, vom fi nevoiţi să ne mulţumim cu mai puţine. Pentru aceasta vom face ipoteze privind constanţa traiectoriei, vom presupune că există totuşi ceva constant în traiectoria respectivă şi că această constanţă poate fi revelată de un număr finit de puncte.
-De exemplu, dacă vom presupune că o anumită traiectorie poate fi parcursă de un anumit mobil fără ca viteza acelui mobil să se modifice, atunci vom descoperi că pentru a determina poziţia ulterioară a mobilului pentru orice moment viitor de timp sunt suficiente doar două puncte distincte. -Dacă vom presupune ceva mai precis că viteza nu este constantă şi că este constantă doar acceleraţia, atunci
--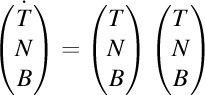
|
|
|
| | | |
|

 . Atunci avem
. Atunci avem  , unde
, unde  .
.  . Dar
. Dar  , unde
, unde  , este
, este 


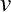 viteza pe elice şi cu
viteza pe elice şi cu 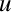 proiecţia acestei viteze pe axă, atunci trebuie să avem relaţiile
proiecţia acestei viteze pe axă, atunci trebuie să avem relaţiile 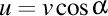 , unde
, unde 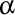 este unghiul dintre tangenta la traiectorie şi axa elicei, deci şi unghiul dintre tangentă şi vectorul lui Darboux. Aşadar, avem mai exact
este unghiul dintre tangenta la traiectorie şi axa elicei, deci şi unghiul dintre tangentă şi vectorul lui Darboux. Aşadar, avem mai exact 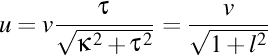 , unde
, unde 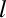 este raportul dintre curbură şi torsiune, adică lancretianul elicei.
este raportul dintre curbură şi torsiune, adică lancretianul elicei. 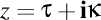 , scris sub formă trigonometrică
, scris sub formă trigonometrică 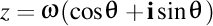 şi construim funcţia numită „derivata Frenet a unui număr complex în raport cu parametrul s” dată prin
şi construim funcţia numită „derivata Frenet a unui număr complex în raport cu parametrul s” dată prin 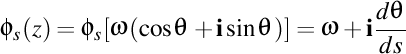 . Această funcţie poate fi aplicată de mai multe ori.
. Această funcţie poate fi aplicată de mai multe ori.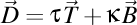 , iar vectorul Darboux de ordinul doi este
, iar vectorul Darboux de ordinul doi este 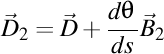 . Deci,
. Deci, 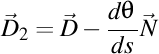 . Putem scrie atunci că
. Putem scrie atunci că 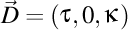 , iar
, iar 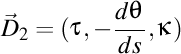 .
. 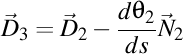 .
.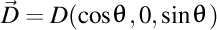 ,
, 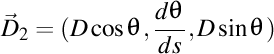 şi
şi 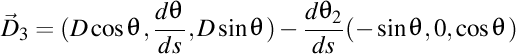 .
.