| | | |
 Home /
Home /
The recurrence theorem of the Frenet formulas 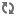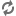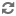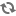 Uploading .... Uploading ....Studying the Frenet formulas I have concluded that they are recursive. More specifically, using the trigonometric form of the Frenet formulas, we proved the following
Theorem: If there is a right trihedron of the n order 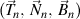
that satisfies the Frenet formulas of the n order, written in the trigonometric form
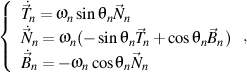
then there is still a right trihedron of the n order
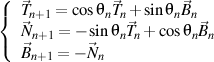
that satisfying, in turn, the Frenet formulas of the n+1 order written also in the trigonometric form
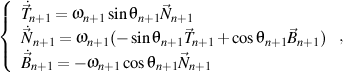
where
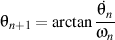 and and 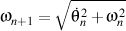
.
Demonstration: Through relations 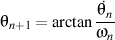 and and 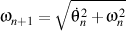
we have that
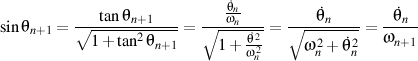
so
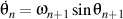
.
We also have
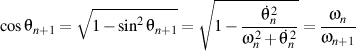
whence
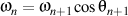
.
Now, we derive the unit vectors of the trihedron of the n+1 order
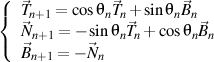
and we obtain
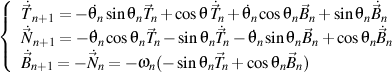
.
Replacing
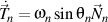
and
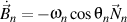
, we obtain
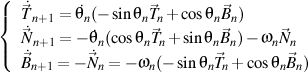
.
But, from the definition of the unit vectors of the high order, we know that
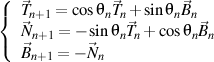
,
so
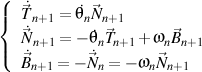
.
Because 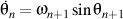 and and 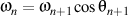 , ,
finally result that
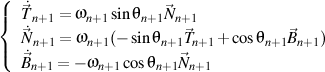
,
qed.
|
|
|
| | | |
|

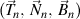
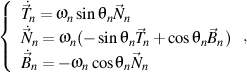
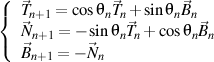
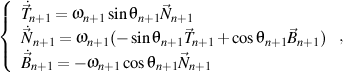
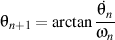 and
and 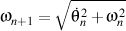
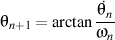 and
and 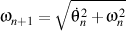
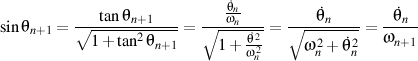
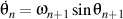
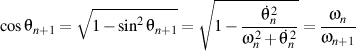
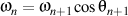
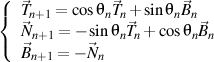
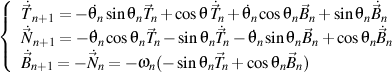
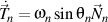
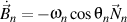
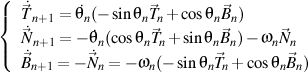
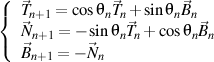
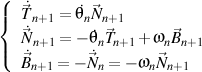
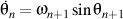 and
and 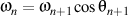 ,
,