| | | |
 Uploading .... Uploading ....
Definiţie
Elicea (propriu-zisă) sau elicea de ordinul întâi este o curbă din spaţiu pentru care orice tangentă la curbă face acelaşi unghi cu o dreaptă fixă, numită axa elicei. Unghiul dintre tangentă şi axă se numeşte unghiul elicei.
Elicea de ordinul n se poate defini prin recurenţă. Dreapta este o elice de ordinul zero, elicea propriu-zisă este o elice de ordinul unu, iar o elice de ordinul n>0 este o curbă a cărei tangentă face peste tot un unghi constant cu tangenta unei elice de ordinul n-1. O definiţie echivalentă a elicei de ordinul n este următoarea: numim elice de ordinul n (în condiţiile în care elicea de ordinul 0 este o dreaptă) o curbă al cărei vector Darboux este mereu tangent la o elice de ordin n-1.
Conform teoremei lui Lancret, condiţia necesară şi suficientă pentru ca o curbă să fie elice este ca raportul dintre curbură şi torsiune (adică lancretianul) să fie constant. Această teoremă ne permite să scriem formulele lui Frenet sub formă trigonometrică, fiindcă putem asocia raportului tocmai unghiul dintre tangentele adiacente. Aşadar, o transformare conformă nu poate modifica ordinul unei elice.
Conform teoremei de recurenţă a formulelor lui Frenet, orice traiectorie pe care o poate avea un corp este o elice de un anumit ordin finit.
Caracteristici
Elicea (de ordinul întâi) este cea mai simplă curbă nedegenerată din spaţiu.
Exemple:
-dreapta este un caz particular de elice (elice de ordinul zero) pentru care raportul dintre curbură şi torsiune (deci şi unghiul elicei) este nul. Dreapta este o elice degenerată.
Viteza unghiulară cu care se roteşte triedrul lui Frenet (sau vectorul lui Darboux asociat) al unei elice circulare este constantă atât în direcţie, cât şi în modul. Viteza unghiulară a triedrului Frenet asociat unei elice oarecare este constantă numai în direcţie, dar nu neapărat şi în modul.
Dacă vectorul lui Darboux asociat elicei este constant şi în modul, elicea este circulară.
În general, viteza unghiulară a triedrului Frenet nu este constantă nici în direcţie, nici în modul.
În baza teoremei de recurenţă a formulelor lui Frenet, orice curbă este, în ultimă instanţă, o elice de ordinul n.
Punctul de vedere geometric.
Din punct de vedere geometric, elicea este definită de doi parametri: curbură şi torsiune, al căror raport este constant.
Punctul de vedere cinematic.
Din punct de vedere cinematic, ne interesează proprietăţile unui mobil care se deplasează cu o anumită viteză cunoscută pe o elice de curbură şi torsiune cunoscute.
Punctul de vedere dinamic.
Asupra unui punct material care se deplasează cu viteză constantă în modul pe o elice acţionează o forţă.
Elicea circulară dreaptă este definită de ecuaţia carteziană
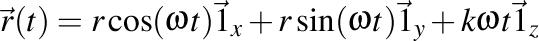 . Curbură . Curbură 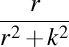 , torsiune , torsiune 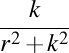 , lancretian , lancretian 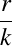 , darbuzian , darbuzian 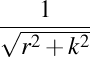 . .
Alte tipuri de elice sunt exemplificate mai jos:
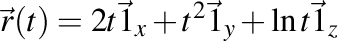 . Curbură . Curbură 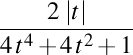 , torsiune , torsiune 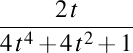 , lancretian , lancretian 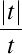 , darbuzian , darbuzian 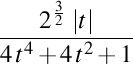 . .
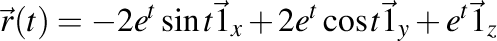 . Curbură . Curbură 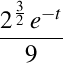 , torsiune , torsiune 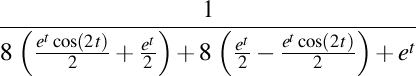 , lancretian , lancretian 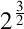 , darbuzian , darbuzian 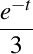 . .
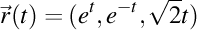 . Elice de curbură . Elice de curbură 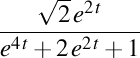 , torsiune , torsiune 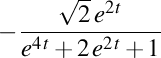 , lancretian , lancretian 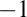 , darbuzian , darbuzian 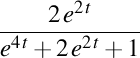 . .
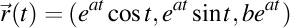 . Elice de curbură . Elice de curbură 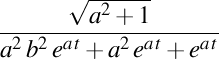 , torsiune , torsiune 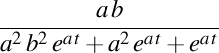 , lancretian , lancretian 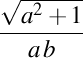 , darbuzian , darbuzian 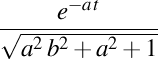 . .Calculele sunt făcute cu Maxima 11.08.0.
Elice constantă: elice ale cărei curbură şi torsiune sunt constante.
Elice variabilă: elice ale cărei curbură şi torsiune sunt variabile, deşi raportul dintre curbură şi torsiune se menţine constant.
Elice periodică: elice ale cărei curbură şi torsiune sunt funcţii periodice de timp.
Elice sinusoidală: elice pentru care curbura (şi torsiunea) este funcţie sinusoidală de timp între două valori, una minimă (asociată unui nod) şi alta maximă (asociată unui ventru). Elicea sinusoidală este cel mai important tip de elice, deoarece, conform proprietăţilor Fourier, orice alt tip de elice este o combinaţie de elice sinusoidale. Elicei sinusoidale îi putem asocia distanţa dintre două noduri sau dintre două ventre. Această distanţă poate fi numită modulul elicei. Prin aceasta, elicea sinusoidală este caracterizată de trei scalari: curbură, torsiune şi modul. Modulul unei elice constante este infinit.
|
|
|
| | | |
|

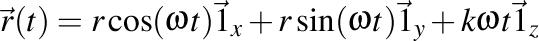 .
. 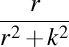
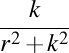
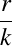
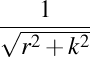
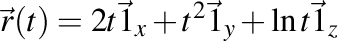 . Curbură
. Curbură 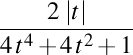 , torsiune
, torsiune 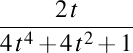 , lancretian
, lancretian 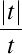 , darbuzian
, darbuzian 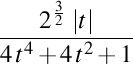 .
.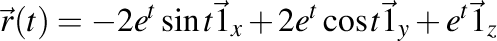 .
. 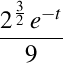
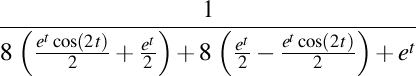
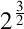
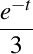
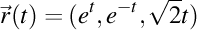 .
. 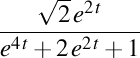
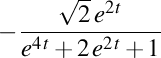
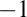
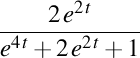
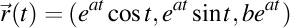 .
.