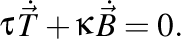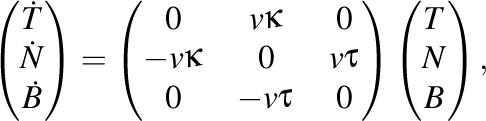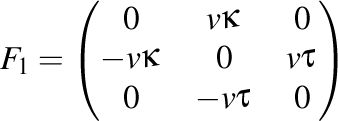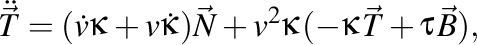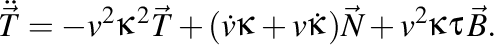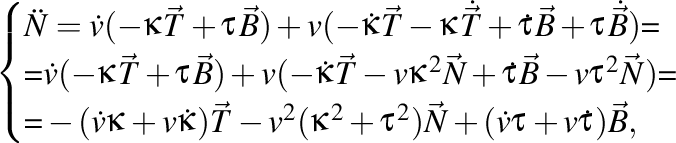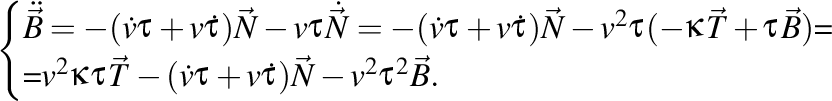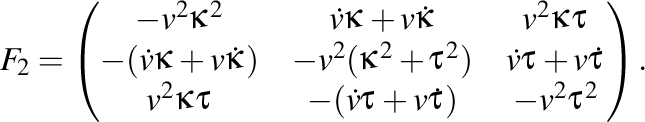Având în vedere importanţa covârşitoare a formulelor lui Frenet în Fizică, este important să ne reamintim câteva detalii legate de acestea.
În cea mai generală situaţie, orice corp se deplasează pe o curbă strâmbă (deci o curbă care nu este neapărat plană). Dacă asociem fiecărui moment de timp vectorul de poziţie al corpului determinat într-un reper ortonormal drept, atunci obţinem legea lui de mişcare, dată de
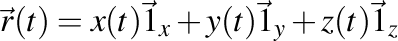 .
.
Voi nota cu un punct superior (aşa cum se obişnuieşte de la Newton încoace) derivata în raport cu timpul şi voi presupune (aşa cum este normal pentru orice corp din Univers) că funcţia de poziţie poate fi derivată de cel puţin trei ori.
În aceste condiţii, formulele lui Frenet particulare (adică raportate la lungimea arcului de curbă) pot fi găsite pe wikipedia. Eu voi prezenta aici formulele lui Frenet generale (adică raportate la parametrul temporal, nu la lungimea arcului de curbă). Oricând se doreşte trecerea de la formulele generale la cele particulare este suficient să se considere că modulul vitezei este egal cu unitatea, adică 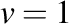 , caz în care toate formulele generale se transformă în formulele particulare.
, caz în care toate formulele generale se transformă în formulele particulare.
Aveţi mai jos formulele Frenet generale, în toată splendoarea lor:
 .
.
Aici vectorii unitari
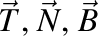
sunt versorii triedrului Frenet (tangenta, normala şi, respectiv, binormala), 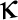 este curbura traiectoriei,
este curbura traiectoriei, 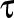 este torsiunea ei, iar vectorul
este torsiunea ei, iar vectorul 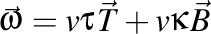 este tocmai viteza unghiulară cu care se roteşte triedrul Frenet. Observaţi un lucru extrem de important: din faptul că nu are componentă pe normală rezultă că viteza unghiulară este întotdeauna perpendiculară pe normală.
este tocmai viteza unghiulară cu care se roteşte triedrul Frenet. Observaţi un lucru extrem de important: din faptul că nu are componentă pe normală rezultă că viteza unghiulară este întotdeauna perpendiculară pe normală.
De curiozitate să calculăm derivata vitezei unghiulare
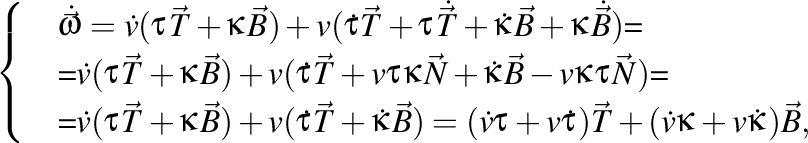
deci acceleraţia unghiulară (viteza de variaţie a vitezei unghiulare) este 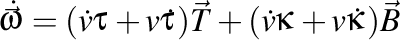
şi este, în continuare, perpendiculară pe normală!
Oare şi restul derivatelor sunt perpendiculare pe normală? Păi, să vedem. Avem
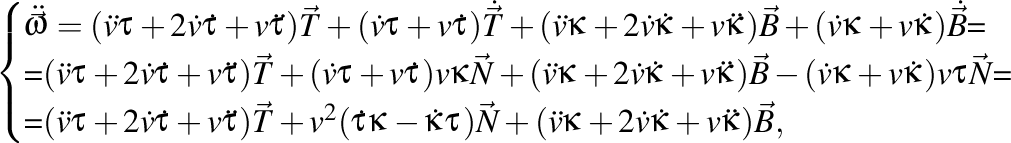
deci derivata următoare nu mai este perpendiculară pe normală  .
.
Să calculăm acum derivatele de ordin superior ale vitezei (deci acceleraţia şi supraacceleraţia). Avem
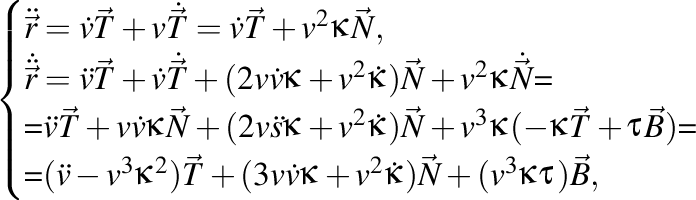
deci
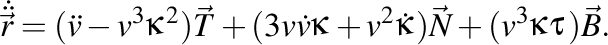
Mai avem relaţiile fascinante
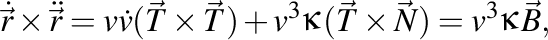
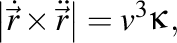
deci
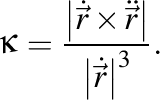
Apoi
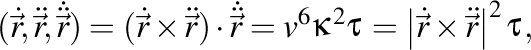
deci
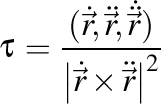 .
.
O altă relaţie extrem de interesantă este următoarea
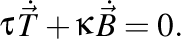
Formulele lui Frenet pot fi scrise matriceal astfel
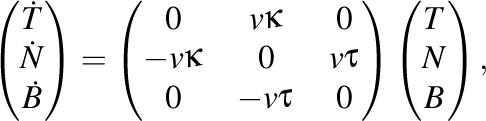
deci putem nota cu
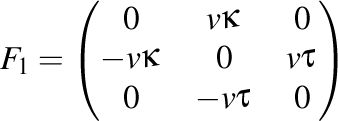
prima matrice Frenet.
În fine, putem determina şi a doua matrice a lui Frenet.
A doua derivată a tangentei este
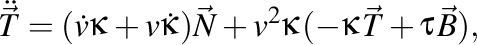
deci, reordonând termenii, obţinem
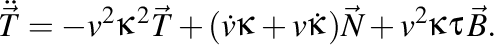
Pentru normală avem
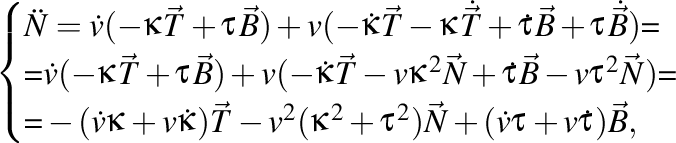
iar pentru binormală avem
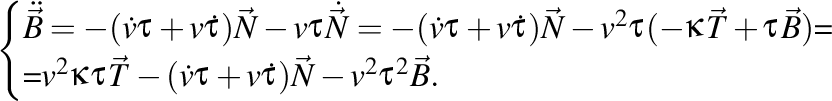
Atunci, a doua matrice a lui Frenet este
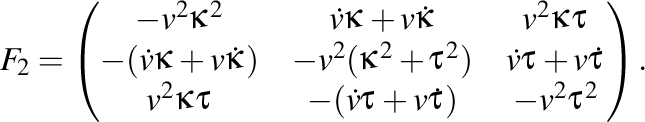

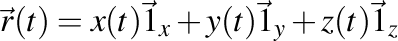 .
.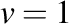 , caz în care toate formulele generale se transformă în formulele particulare.
, caz în care toate formulele generale se transformă în formulele particulare. .
. 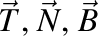
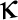 este curbura traiectoriei,
este curbura traiectoriei, 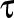 este torsiunea ei, iar vectorul
este torsiunea ei, iar vectorul 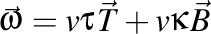 este tocmai viteza unghiulară cu care se roteşte triedrul Frenet. Observaţi un lucru extrem de important: din faptul că nu are componentă pe normală rezultă că
este tocmai viteza unghiulară cu care se roteşte triedrul Frenet. Observaţi un lucru extrem de important: din faptul că nu are componentă pe normală rezultă că 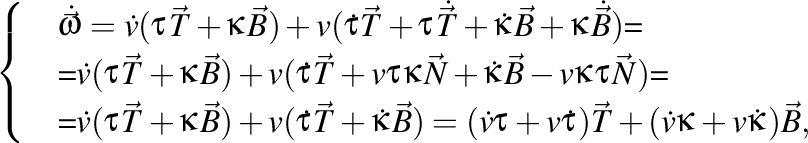
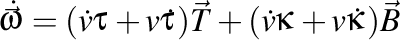
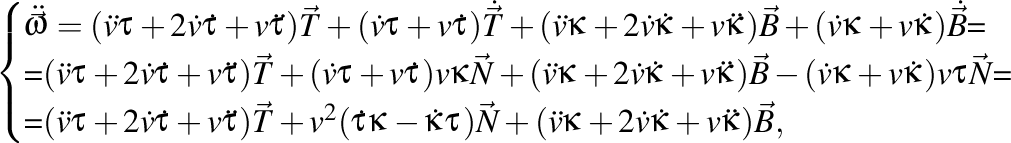
 .
. 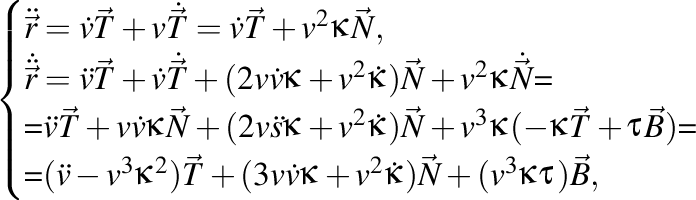
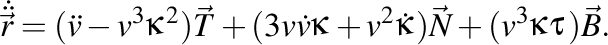
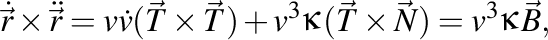
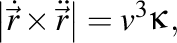
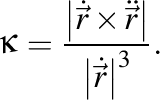
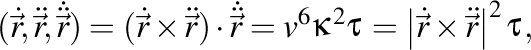
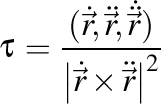 .
.