| | | |
 Uploading .... Uploading ....În Fizica elicoidală toate corpurile sunt alcătuite din luxoni, adică din particule fără masă de repaus care se deplasează cu viteza luminii în vid.
Să arătăm că viteza este strâns legată de lancretian. Prin aceasta arătăm că modificarea modulului vitezei nu se poate face decât cu modificarea lancretianului.
Să presupunem că un luxon se deplasează cu viteza c de-a lungul unei elice de ecuaţii
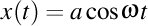 , , 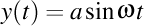 , , 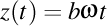 . .
Viteza luxonului va fi un vector de componente 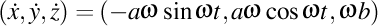 . Modulul acestui vector trebuie să fie egal cu viteza luminii în vid, aşadar avem . Modulul acestui vector trebuie să fie egal cu viteza luminii în vid, aşadar avem 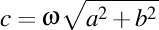 . Observăm că proiecţia luxonului pe axa OZ are viteza . Observăm că proiecţia luxonului pe axa OZ are viteza 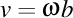 . Înlocuindu-l pe . Înlocuindu-l pe 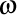 din expresia din expresia 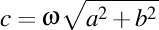 obţinem că proiecţia luxonului pe axa OZ are viteza obţinem că proiecţia luxonului pe axa OZ are viteza 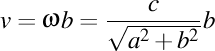 . Dar ştim că valorile curburii şi a torsiunii elicei sunt date de expresiile . Dar ştim că valorile curburii şi a torsiunii elicei sunt date de expresiile 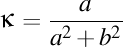 şi respectiv şi respectiv 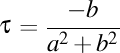 . Aşadar, lancretianul elicei este . Aşadar, lancretianul elicei este 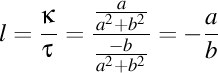 . Putem rescrie atunci viteza proiecţiei luxonului pe axa OZ ca fiind . Putem rescrie atunci viteza proiecţiei luxonului pe axa OZ ca fiind 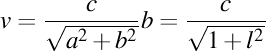 . Aşadar, proiecţia vitezei luxonului pe axa OZ nu depinde de valorile separate ale curburii şi torsiunii, ci doar de raportul lor, adică doar de valoarea lancretianului. . Aşadar, proiecţia vitezei luxonului pe axa OZ nu depinde de valorile separate ale curburii şi torsiunii, ci doar de raportul lor, adică doar de valoarea lancretianului.
Prin urmare, orice transformare a traiectoriei luxonului care nu modifică lancretianul, nu va modifica nici modulul vitezei proiecţiei pe axă.
Deci, ca să putem modifica modulul vitezei proiecţiei va trebui să modificăm şi lancretianul traiectoriei. Dar modificarea lancretianului duce la devierea traiectoriei de la o elice (şi încadrarea ei într-o elice de ordinul doi), deci viteza de ordinul doi a luxonului nu-şi poate modifica modulul fără să-şi modifice şi direcţia. Dacă modificarea direcţiei durează puţin, atunci, după ce lancretianul redevine constant, şi viteza de ordinul doi redevine constantă.
Postulăm că masa de mişcare a luxonului este proporţională cu torsiunea traiectoriei.
|
|
|
| | | |
|

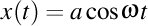 ,
, 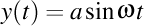 ,
, 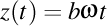 .
. 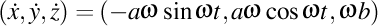 . Modulul acestui vector trebuie să fie egal cu viteza luminii în vid, aşadar avem
. Modulul acestui vector trebuie să fie egal cu viteza luminii în vid, aşadar avem 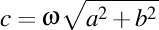 . Observăm că proiecţia luxonului pe axa OZ are viteza
. Observăm că proiecţia luxonului pe axa OZ are viteza 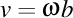 . Înlocuindu-l pe
. Înlocuindu-l pe 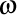 din expresia
din expresia 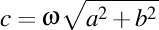 obţinem că proiecţia luxonului pe axa OZ are viteza
obţinem că proiecţia luxonului pe axa OZ are viteza 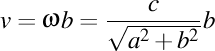 . Dar ştim că valorile curburii şi a torsiunii elicei sunt date de expresiile
. Dar ştim că valorile curburii şi a torsiunii elicei sunt date de expresiile 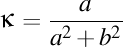 şi respectiv
şi respectiv 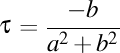 . Aşadar, lancretianul elicei este
. Aşadar, lancretianul elicei este 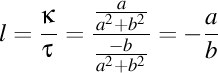 . Putem rescrie atunci viteza proiecţiei luxonului pe axa OZ ca fiind
. Putem rescrie atunci viteza proiecţiei luxonului pe axa OZ ca fiind 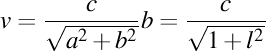 . Aşadar, proiecţia vitezei luxonului pe axa OZ nu depinde de valorile separate ale curburii şi torsiunii, ci doar de raportul lor, adică doar de valoarea lancretianului.
. Aşadar, proiecţia vitezei luxonului pe axa OZ nu depinde de valorile separate ale curburii şi torsiunii, ci doar de raportul lor, adică doar de valoarea lancretianului. 