| | | |
 Uploading .... Uploading ....Triedrul complementar al lui Frenet (sau triedrul lui Darboux, cu condiţia ca acesta să nu fie confundat cu triedrul geodezic) este triedrul format de următorii trei versori:
-versorul vitezei unghiulare a triedrului Frenet (care coincide cu versorul vectorului lui Darboux);
-versorul produsului vectorial dintre viteza unghiulară a triedrului Frenet şi derivata acestei viteze unghiulare. Acest versor este coliniar cu normala triedrului Frenet, deoarece, atât viteza unghiulară, cât şi derivata ei sunt ambele perpendiculare pe normală.
-produsul vectorial al versorilor anteriori.
Triedrul complementar al lui Frenet are proprietăţile lui Frenet, fapt pentru care triedrul complementar al lui Frenet are şi el, la rândul său, un triedru complementar. Această recurenţă este demonstrată de teorema de recurenţă a formulelor lui Frenet.
În funcţie de versorii triedrului Frenet, versorii triedrului complementar al lui Frenet sunt
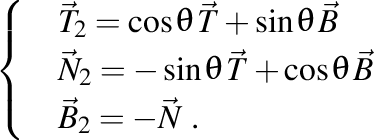
Aici avem 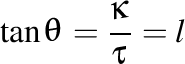 , adică , adică 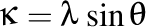 şi şi 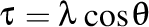 cu cu 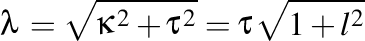 . .
În funcţie de curbură şi torsiune mai putem scrie că triedrul complementar al lui Frenet este dat de versorii
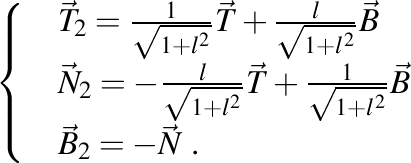 . .
Reciproc, prin inversarea (sau, echivalent, transpunerea) matricei ortogonale anterioare, obţinem că versorii triedrului Frenet în funcţie de versorii tredrului complementar al lui Frenet sunt
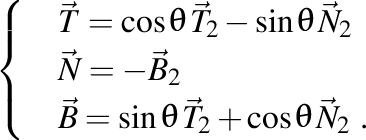
Datorită importanţei acestui triedru pentru Fizica elicoidală, îl vom numi şi triedru natural.
Dacă notăm simbolic triedrul lui Frenet cu 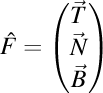 , şi , şi 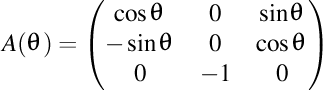 , atunci putem scrie condensat că , atunci putem scrie condensat că 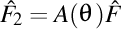 . În general, avem . În general, avem 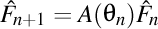 , unde , unde 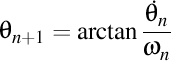 şi şi 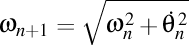 . .
Mai putem face convenţia că orice reper cartezian se roteşte în timp în jurul axei OZ cu viteza unghiulară 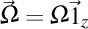 . Această viteză de rotaţie poate reprezenta de asemenea tot prin convenţie tocmai viteza cu care trece timpul în sistemul cartezian respectiv. Asemenea convenţii ne-ar permite să facem o legătură directă între reperul cartezian şi reperul Frenet. În plus, convenţia făcută asupra reperului cartezian ne-ar spune că punctele acestui reper descriu cercuri (oare n-ar trebui să descrie elice?). Mai trebuie aprofundată posibilitatea introducerii vitezei luminii printre aceste consideraţii. . Această viteză de rotaţie poate reprezenta de asemenea tot prin convenţie tocmai viteza cu care trece timpul în sistemul cartezian respectiv. Asemenea convenţii ne-ar permite să facem o legătură directă între reperul cartezian şi reperul Frenet. În plus, convenţia făcută asupra reperului cartezian ne-ar spune că punctele acestui reper descriu cercuri (oare n-ar trebui să descrie elice?). Mai trebuie aprofundată posibilitatea introducerii vitezei luminii printre aceste consideraţii.
Reperul cartezian diferă de toate celelalte repere prin faptul că el cuprinde ca reper unic toate celelalte traiectorii, în sensul că pentru toate traiectoriile posibile există un ordin finit astfel încât reperul Frenet de ordinul respectiv coincide tocmai cu reperul cartezian. Prin aceasta am convenit să considerăm că reperul cartezian este reperul Frenet de ordin maxim posibil. Pe scurt, reperul cartezian este un reper Frenet.
(1110091032). Dacă derivăm versorii triedrului complementar, obţinem
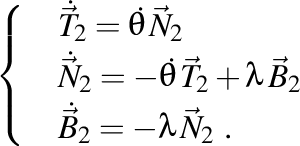
De aici rezultă că a doua torsiune complexă este 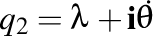 . Dar ştim că prima torsiune este . Dar ştim că prima torsiune este 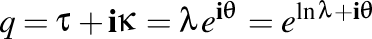 . Deci, . Deci, 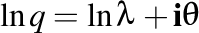 . Ne rămâne acum să investigăm relaţia interesantă dintre . Ne rămâne acum să investigăm relaţia interesantă dintre 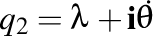 şi şi 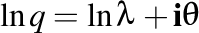 . .
|
|
|
| | | |
|

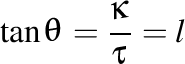 , adică
, adică 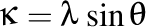 şi
şi 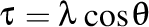 cu
cu 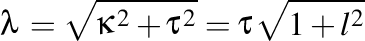 .
.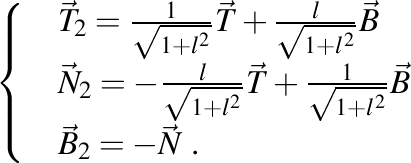 .
.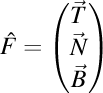 , şi
, şi 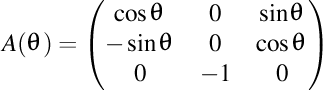 , atunci putem scrie condensat că
, atunci putem scrie condensat că 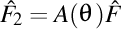 . În general, avem
. În general, avem 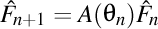 , unde
, unde 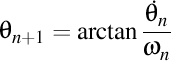 şi
şi 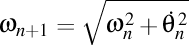 .
.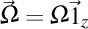 . Această viteză de rotaţie poate reprezenta de asemenea tot prin convenţie tocmai viteza cu care trece timpul în sistemul cartezian respectiv. Asemenea convenţii ne-ar permite să facem
. Această viteză de rotaţie poate reprezenta de asemenea tot prin convenţie tocmai viteza cu care trece timpul în sistemul cartezian respectiv. Asemenea convenţii ne-ar permite să facem 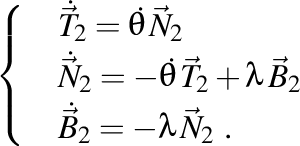
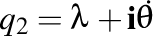 . Dar ştim că prima torsiune este
. Dar ştim că prima torsiune este 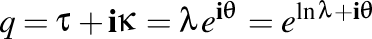 . Deci,
. Deci, 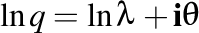 . Ne rămâne acum să investigăm relaţia interesantă dintre
. Ne rămâne acum să investigăm relaţia interesantă dintre 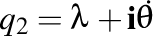 şi
şi 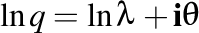 .
.